밀만의 정리 (Millman’s Theorem) 에 대해 알아보겠습니다.
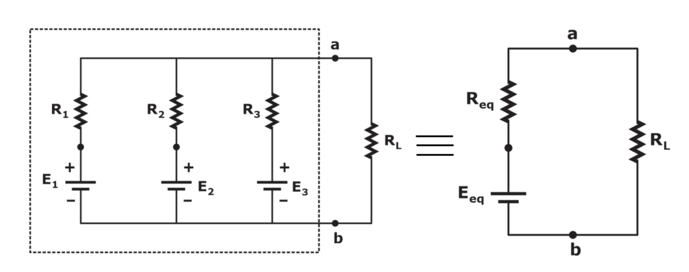
먼저 아래의 그림에서 왼쪽의 복잡한 회로를 오른쪽의 간단한 회로로 변환을 하면 a~b에 걸리는 전압과 전류를 쉽게 구할 수 있습니다.
밀만의 정리에 따르면 각 전압원과 저항은 전류를 생성성하며 이때 모든 전류의 합은 전체 전류의 총전류와 같습니다.
i = i1 + i2 + i3 + ... + in
전류의 기본공식인 V = I x Z이나 쉽게 V = I X R을 생각해 보겠습니다. (전압 =전류 x 임피던스 또는 전압 = 전류 x 저항)
또한 Z = 1 / Y라는 것을 알고 있으면, 반대로 Y = 1 / Z로 바꿀 수 있습니다.
Z대신 R로 표현하고 싶을 때는 R의 역수인 컨덕턴스 G를 이용해서 G = 1 / R 이므로 R = 1 / G로 표현할 수 있습니다.
위의 그림에서 임피던스 Z에는 R밖에 없으므로 1 / Z나 1 / R이나 동일하게 사용됩니다.
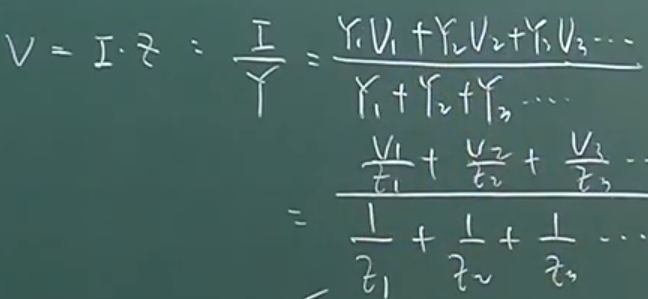
따라서 맨 위의 그림을 풀어쓰면
E_eq는 다음과 같이 쓸 수 있습니다.

그리고 R_eq는 다음과 같습니다.

그럼 실제 예제를 통해 밀만의 정리를 알아보겠습니다.
아래와 같은 회로에서 맨왼쪽의 R_L에 흐르는 전류 I_L와 전업 V_L을 구해보겠습니다.

우선 각 전류를 구하면

여기서 유의할 점은 전압 E1의 방향이 반대이기 때문에 전류 I1은 (-) 값이 나왔다는 것입니다.
따라서 전체 흐르는 전류는 -20/2 + 10/3 + 8/4 = -56/12[A]입니다.
다음은 저항 R_eq를 구해보겠습니다.
1/R_eq = 1/2 + 1/3 + 1/4 = 13/12이므로 R_eq = 12/13입니다.
따라서 E_eq = I_eq / R_eq = -56/13 [V]이 됩니다.
이것을 그림으로 간단히 표현하면 다음과 같습니다.

이제 전체에 흐르는 전압과 저항을 통해 전류를 구해보겠습니다.
I = E / R = (56/13) / (12/13 + 5) = -0.727 [A]
마지막으로 a~b 사이의 전압은 V = I x R 공식을 사용하여
V= -0.727 x 5 = -3.635 [V]
이렇게 계산할 수 있습니다.
시뮬레이션 프로그램으로 검증을 해보았습니다.
위 예제처럼 저항 3개와 전압원 3개를 배치하고 맨 우측에 저항을 배치하여 이 곳의 저항을 측정해보았더니 아래와 같이 나타났습니다.

위 그림처럼 3.636V로 나타났습니다. 부호가 반대인것은 전압의 방향이므로 참고하시면 되겠습니다.
아래는 실제 시뮬레이션 한 결과입니다.
이상으로 밀만의 정리에 대해 살펴보았습니다.
※ 함께 보면 좋은 글
중첩의 원리 쉽게 이해하기 principle of superposition
회로이론에서 중첩의 원리를 쉽게 설명하면 다수의 전압원과 전류원이 존재할 때 회로의 각 부분의 전류는 전압원 또는 전류원이 하나일 때 흐르는 전류의 합과 같다는 것입니다. 간단히 정리
pridjoo.tistory.com
테브난의 정리 쉽게 이해하기 Thevenin's theorem
테스난의 정리 처음에 접할 때는 어려워 보이기도 하지만 익숙해지면 정말 회로이론에서 정말 쉽게 문제를 풀 수 있는 방법입니다. 테브난의 정리는 쉽게 정리하면 복한 회로를 한개의 전압원
pridjoo.tistory.com
노튼의 정리 쉽게 이해하기 Norton's theorem
회로이론에서 테브난의 정리와 함께 자주 언급 되는 것이 노튼의 정리입니다. 오늘은 노튼의 정리에 대해 알아보겠습니다. 둘은 서로 쌍대관계에 있다고 할 수 있습니다. 노튼의 정리 노튼의 정
pridjoo.tistory.com
이상 밀만의 정리였습니다.
'전기' 카테고리의 다른 글
| 투자율 자화율 자속밀도 자기회로 (1) | 2024.01.03 |
|---|---|
| 직렬리액터, 분로리액터, 한류리액터, 소호리액터, 직류리액터 | 전력 시스템에서의 리액터 종류와 기능 (1) | 2023.11.29 |
| 피뢰기 | 전기 시설의 수호자 (1) | 2023.11.12 |
| 플레밍의 왼손법칙과 직류전동기 (0) | 2023.11.06 |
| 전력계통 안정화 장치 PSS 안정도 향상을 위한 초속응 여자제어 (1) | 2023.11.03 |



